Simulación Numérica
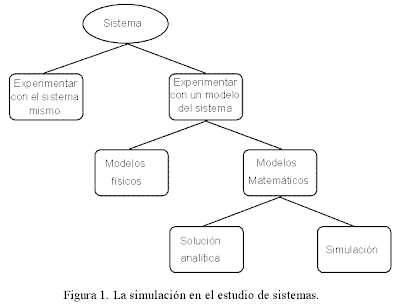
Simulación implica crear un modelo que aproxima cierto aspecto de un sistema del mundo real y que puede ser usado para generar historias artificiales del sistema, de forma tal que nos permite predecir cierto aspecto del comportamiento del sistema.
En particular, usaremos computadores para imitar comportamientos del sistemas evaluando numericamente un modelo del mismo. Estas evaluaciones numericas son las que nos permiten generar las historias artificiales que no son mas que experimentos.
Modelo
Un modelo es una representación de un objeto, idea, o sistema en una forma diferente a la entidad misma. En nuestro caso el modelo es un conjunto de relaciones matemáticas o lógicas derivadas de supuestos sobre el comportamiento del sistema.
¿Para que?
Simulamos para explicar, entender o mejorar el sistema.
Ejemplo:
El diseño de un procesador involucra miles o millones de compuertas lógicas interconectadas. El proceso de crear el primer chip es sumamente costoso y no es posible darse el lujo de construir varios chips y luego verificar su funcionamiento. Lo que se hace es modelar el procesador y verificar su funcionamiento usando simulación.
¿Cuando?
a) El sistema real no existe. Es costoso, peligroso, consume mucho tiempo, o imposible de construir y experimentar con prototipos (nuevo computador o procesador, reactor nuclear).
b) Experimentar con el sistema real es complicado, costoso, peligroso, o puede causar serios desajustes (sistema de transporte, sistema de manufactura, reactor nuclear).
c) Necesidad de estudiar el pasado, presente, o futuro del sistema en tiempo real, tiempo expandido, o tiempo comprimido (sistemas de control a tiempo real, estudios en cámara lenta, crecimiento poblacional).
d) Es sistema es tan complejo que su evaluación analítica es prohibitiva, bien sea porque el modelado matemático es imposible, o porque el modelado matemático no tiene solución analítica o numérica simple y practica (colas de espera, ecuaciones diferenciales no lineales, problemas estocásticos).
e) Se puede validar satisfactoriamente el modelo de simulación.
Se podría decir "Simular cuando todo lo demás falla", pero esto no es excusa para usar simulación inadecuadamente.
Las areas de aplicacion de la simulacion son numerosas y entre ellas estan:
- Diseño y analisis de sistemas de produccion.
- Analisis de sistemas finacieros o economicos.
- Evaluacion de software y hardware.
- Evaluacion de sistemas de armamaneto militar o sistemas tacticos.
- Determinacion de politicas de inventario.
- Manejo de bosques.
- Diseño de sistemas de comunicacion y protocolos
- Diseño de sistemas de transporte.
- Evaluacion de diseños de organizaciones como hospitales, comedores, servicios de correo, etc.
I. Errores comunes en simulación
1. Nivel de detalle inapropiado
Un modelo analítico es menos detallado que un modelo de simulación. Análisis requiere de muchos supuestos y simplificaciones. El detalle en un modelo de simulación esta limitado por el tiempo disponible para desarrollarlo.
Mas detalle -> más tiempo -> incrementa la posibilidad de errores y es mas difícil detectarlos -> incrementa el tiempo de corrida del modelo
¡Mas detalle no necesariamente es mejor!
Mas detalle requiere mas conocimiento de los parámetros de entrada, que si no están disponibles pueden hacer el modelo mas inexacto.
Ejemplo:
Supongamos que en la simulación de un sistema de tiempo compartido (timesharing) debemos simular el tiempo requerido para satisfacer accesos a disco. Una opción es generarlos usando una distribución exponencial. Una alternativa mas detallada seria simular el movimiento de los cabezales y la rotación del disco. En la segunda alternativa se pueden tener mejores resultados solo si conocemos las referencias a sectores y pistas. Sin embargo, si esta información no esta disponible a la hora de la entrada de datos, hay que terminar generándolos exponencialmente y hubiese sido menos costoso irse por la primera alternativa.
Es mejor partir de un modelo sencillo, obtener resultados, estudiar la sensibilidad, e introducir mas detalles en las áreas que impactan mas los resultados.
2. Lenguaje inapropiado
Lenguajes de simulación de propósito especial requieren menos tiempo para implementar el modelo y facilitan actividades como verificación (mediante el uso de opciones de trazado) y de análisis estadístico. Lenguajes de propósito general son mas portables y proveen mejor control sobre la eficiencia y el tiempo de corrida de la simulación.
3. Modelos no verificados
Los modelos de simulación son generalmente programas grandes, que si no se tienen las precauciones respectivas, es posible tener errores de programación que hagan las conclusiones sin sentido.
4. Modelos inválidos
Aun cuando no hayan errores de programación, puede que el modelo no represente al sistema real adecuadamente por supuestos incorrectos en su formulación. Es esencial que el modelo sea validado para asegurar que las conclusiones a las que se pueda llegar sean las mismas que se obtendrían del sistema real. Todo modelo de simulación debe estar bajo sospecha hasta que se pruebe lo contrario por modelos analíticos, mediciones, o intuición.
5. Tratamiento incorrecto de las condiciones iniciales
Generalmente la parte inicial de una corrida de simulación no es representativa del comportamiento de un sistema en estado estable, por lo tanto debe ser descartada.
6. Simulaciones muy cortas
Por tratar de ahorrar tiempo de análisis y de computación, las corridas de simulación pueden ser muy cortas. Los resultados en estos casos dependen fuertemente de las condiciones iniciales y pueden no representar al sistema real. El tiempo de corrida adecuado depende de la exactitud deseada (intervalos de confianza) y de la varianza de las cantidades observadas.
7. Generadores de números aleatorios inadecuados
Las simulaciones requieren de cantidades aleatorias que son producidas por procedimientos llamados generadores de números aleatorios. Es mejor usar generadores que han sido bien analizados a usar los de uno mismo. Aun buenos generadores presentan problemas.
8. Selección de semillas inadecuadas
Los generadores de números aleatorios son procedimientos que dado un numero aleatorio generan otro. El primer numero aleatorio de la secuencia es llamado la semilla y debe ser proporcionada por el analista. Las semillas para diferentes secuencias deben ser cuidadosamente seleccionadas para mantener independencia entre las secuencias. Los analistas usualmente usan una misma secuencia para diferentes procesos o usan la misma semilla para todas las secuencias. Esto introduce correlación entre los procesos y puede llevar a conclusiones erróneas.
II. Otras causas del fracaso de los análisis de simulación
1. Estimación inadecuada del tiempo para desarrollar el proyecto
Es común subestimar el tiempo y el esfuerzo requerido para desarrollar modelos de simulación. Si la simulación es exitosa y produce información útil, sus usuarios quieren incorporar mas funciones, parámetros y detalles. Por el contrario, si no provee de información útil, usualmente se espera que al añadir elementos la puedan hacer útil. En ambos casos el proyecto se extiende mas allá de las proyecciones iniciales. Para proyectos grandes se deben hacer previsiones para incorporara cambios que son inevitables sobre largos periodos de tiempo.
2. Metas inalcanzables
La simulación es un proceso largo y complejo y se debe tener claramente definido un conjunto de metas que sean especificas, minuciosas, medibles, y alcanzables.
Un ejemplo común de una meta inalcanzable es "modelemos X." Es posible modelar muchas características diferentes de X a muchos niveles de detalle.
3. Mezcla incompleta de habilidades
Un proyecto de simulación requiere por lo menos:
a. Liderazgo: Habilidad para motivar, guiar y manejar a los miembros del equipo de simulación.
b. Modelaje y estadísticas: Habilidad para identificar las características claves del sistema y modelarlas al nivel de detalle requerido.
c. Programación: Habilidad para escribir código entendible y verificable que implemente el modelo correctamente.
d. Conocimiento del sistema modelado: Habilidad para entender el sistema, explicarlo al equipo de modelaje, e interpretar los resultados del modelo en términos de su impacto en el diseño del sistema.
4. Nivel inadecuado de participación de los usuarios
Es esencial que el equipo de simulación y los usuarios de la organización estén en constante contacto para intercambiar y discutir ideas. La mayoría de los sistemas evolucionan y cambian con el tiempo y un modelo desarrollado sin la participación de los usuarios raramente resulta exitoso.
5. Documentación inexistente u obsoleta
La mayoría de los modelos de simulación se desarrollan en largos periodos de tiempo y continuamente son modificados a medida que el sistema cambia o es mejor comprendido. Su documentación muchas veces es desatendida y rápidamente se vuelve obsoleta. Es recomendable documentar los programas y usar lenguajes que sean fáciles de leer.
6. Inhabilidad para gerenciar el desarrollo de programas de computación grandes
Hay muchas herramientas de ingeniería de la programación que permiten vigilar los objetivos del diseño, los requerimientos funcionales, las estructuras de datos y los estimados de progreso. También hay un conjunto de principios de diseño, como diseño de arriba abajo y programación estructurada, para desarrollar grandes proyectos en forma ordenada . Sin el uso de estas herramientas y técnicas es imposible desarrollar exitosamente un modelo de simulación grande.
7. Resultados misteriosos
Resultados misteriosos generalmente son debido a errores de programación, supuestos incorrectos en el modelo, o falta de entendimiento del sistema real. Nunca deben ser obviados.
III. Terminología
1. Variables de Estado
El estado del sistema esta caracterizado por el valor que tengan las variables de estado en un instante de tiempo dado. El conjunto de variables de estado debe ser suficiente para el propósito de estudio, y puede diferir en el número y tipo de variables si los objetivos de la simulación cambian. Si la simulación es detenida, puede ser continuada después si y solo si los valores de las variables de estado son conocidos.
2. Evento
Un evento es un suceso, un hecho, una ocurrencia que genera un cambio en el estado del sistema. Una llegada, una salida, etc.
3. Modelos de Tiempo Continuo y de Tiempo Discreto
Modelo de Tiempo Continuo
Cuando el estado del sistema esta definido para cada instante de tiempo.
Modelo de Tiempo Discreto
Cuando el estado del sistema esta definido solo para particulares instantes de tiempo.
4. Modelos de Estado Continuo y de Estado Discreto
El modelo es de estado continuo o discreto dependiendo de si las variables de estado son continuas o discretas.
Modelo de Estado Discreto → Modelo de Eventos Discretos
Modelo de Estado Continuo → Modelo de Eventos Continuos
Continuidad de tiempo no implica continuidad de estado y viceversa.
5. Modelos Determinísticos y Probabilísticos
Si los resultados de un modelo pueden predecirse con certeza, el modelo es determinístico; un simulador de contratos colectivos. Si repeticiones con la misma entrada pueden producir resultados distintos entonces el modelo es probabilístico; un simulador de colas.
6. Modelos Estáticos y Dinámicos
Un modelo en el que el tiempo no es una variable es estático. Si el sistema cambia con el tiempo el modelo es dinámico.
E = m c2 → Modelo Estático (materia en energía) Numero de trabajos en cola en un computador. → Modelo Dinámico
7. Modelos Lineales y No-Lineales
Si la salida es una función lineal de la entrada, el modelo es lineal, de lo contrario es no-lineal.
Ejemplo:
8. Modelos Cerrados y Abiertos
Si la entrada es externa al modelo e independiente de el, el modelo es abierto. Si el modelo es cerrado no hay entrada externa. Puede depender de los objetivos de la simulación, como se enfoque el problema y los supuestos que se hagan. Por ejemplo: podemos simular el trafico en una ciudad como un sistema cerrado si asumimos que el numero de vehículos permanece constante (no hay arribos ni salidas o arribos = salidas), o como un sistema abierto generando arribos y salidas al exterior.
9. Modelo Estables e Inestables
Si el comportamiento del sistema converge a un estado estable (independientemente del tiempo) el modelo es estable. Un modelo cuyo comportamiento cambia constantemente es inestable. Por ejemplo, en un sistema de taquilla simple tenemos:
Intervalo entre llegadas >tiempo de servicio → modelo estable
Intervalo entre llegadas ≤tiempo de servicio → modelo inestable.
Ejemplo
Modelos de sistema de computación generalmente son de tiempo continuo, estado discreto, probabilísticos, dinámicos y no-lineales. Algunos son abiertos y otros cerrados. También pueden ser estables o inestables.
Fuente: Prof. Herbert Hoeger. http://webdelprofesor.ula.ve/ingenieria/hhoeger
En particular, usaremos computadores para imitar comportamientos del sistemas evaluando numericamente un modelo del mismo. Estas evaluaciones numericas son las que nos permiten generar las historias artificiales que no son mas que experimentos.
Modelo
Un modelo es una representación de un objeto, idea, o sistema en una forma diferente a la entidad misma. En nuestro caso el modelo es un conjunto de relaciones matemáticas o lógicas derivadas de supuestos sobre el comportamiento del sistema.
¿Para que?
Simulamos para explicar, entender o mejorar el sistema.
Ejemplo:
El diseño de un procesador involucra miles o millones de compuertas lógicas interconectadas. El proceso de crear el primer chip es sumamente costoso y no es posible darse el lujo de construir varios chips y luego verificar su funcionamiento. Lo que se hace es modelar el procesador y verificar su funcionamiento usando simulación.
¿Cuando?
a) El sistema real no existe. Es costoso, peligroso, consume mucho tiempo, o imposible de construir y experimentar con prototipos (nuevo computador o procesador, reactor nuclear).
b) Experimentar con el sistema real es complicado, costoso, peligroso, o puede causar serios desajustes (sistema de transporte, sistema de manufactura, reactor nuclear).
c) Necesidad de estudiar el pasado, presente, o futuro del sistema en tiempo real, tiempo expandido, o tiempo comprimido (sistemas de control a tiempo real, estudios en cámara lenta, crecimiento poblacional).
d) Es sistema es tan complejo que su evaluación analítica es prohibitiva, bien sea porque el modelado matemático es imposible, o porque el modelado matemático no tiene solución analítica o numérica simple y practica (colas de espera, ecuaciones diferenciales no lineales, problemas estocásticos).
e) Se puede validar satisfactoriamente el modelo de simulación.
Se podría decir "Simular cuando todo lo demás falla", pero esto no es excusa para usar simulación inadecuadamente.
Las areas de aplicacion de la simulacion son numerosas y entre ellas estan:
- Diseño y analisis de sistemas de produccion.
- Analisis de sistemas finacieros o economicos.
- Evaluacion de software y hardware.
- Evaluacion de sistemas de armamaneto militar o sistemas tacticos.
- Determinacion de politicas de inventario.
- Manejo de bosques.
- Diseño de sistemas de comunicacion y protocolos
- Diseño de sistemas de transporte.
- Evaluacion de diseños de organizaciones como hospitales, comedores, servicios de correo, etc.
I. Errores comunes en simulación
1. Nivel de detalle inapropiado
Un modelo analítico es menos detallado que un modelo de simulación. Análisis requiere de muchos supuestos y simplificaciones. El detalle en un modelo de simulación esta limitado por el tiempo disponible para desarrollarlo.
Mas detalle -> más tiempo -> incrementa la posibilidad de errores y es mas difícil detectarlos -> incrementa el tiempo de corrida del modelo
¡Mas detalle no necesariamente es mejor!
Mas detalle requiere mas conocimiento de los parámetros de entrada, que si no están disponibles pueden hacer el modelo mas inexacto.
Ejemplo:
Supongamos que en la simulación de un sistema de tiempo compartido (timesharing) debemos simular el tiempo requerido para satisfacer accesos a disco. Una opción es generarlos usando una distribución exponencial. Una alternativa mas detallada seria simular el movimiento de los cabezales y la rotación del disco. En la segunda alternativa se pueden tener mejores resultados solo si conocemos las referencias a sectores y pistas. Sin embargo, si esta información no esta disponible a la hora de la entrada de datos, hay que terminar generándolos exponencialmente y hubiese sido menos costoso irse por la primera alternativa.
Es mejor partir de un modelo sencillo, obtener resultados, estudiar la sensibilidad, e introducir mas detalles en las áreas que impactan mas los resultados.
2. Lenguaje inapropiado
Lenguajes de simulación de propósito especial requieren menos tiempo para implementar el modelo y facilitan actividades como verificación (mediante el uso de opciones de trazado) y de análisis estadístico. Lenguajes de propósito general son mas portables y proveen mejor control sobre la eficiencia y el tiempo de corrida de la simulación.
3. Modelos no verificados
Los modelos de simulación son generalmente programas grandes, que si no se tienen las precauciones respectivas, es posible tener errores de programación que hagan las conclusiones sin sentido.
4. Modelos inválidos
Aun cuando no hayan errores de programación, puede que el modelo no represente al sistema real adecuadamente por supuestos incorrectos en su formulación. Es esencial que el modelo sea validado para asegurar que las conclusiones a las que se pueda llegar sean las mismas que se obtendrían del sistema real. Todo modelo de simulación debe estar bajo sospecha hasta que se pruebe lo contrario por modelos analíticos, mediciones, o intuición.
5. Tratamiento incorrecto de las condiciones iniciales
Generalmente la parte inicial de una corrida de simulación no es representativa del comportamiento de un sistema en estado estable, por lo tanto debe ser descartada.
6. Simulaciones muy cortas
Por tratar de ahorrar tiempo de análisis y de computación, las corridas de simulación pueden ser muy cortas. Los resultados en estos casos dependen fuertemente de las condiciones iniciales y pueden no representar al sistema real. El tiempo de corrida adecuado depende de la exactitud deseada (intervalos de confianza) y de la varianza de las cantidades observadas.
7. Generadores de números aleatorios inadecuados
Las simulaciones requieren de cantidades aleatorias que son producidas por procedimientos llamados generadores de números aleatorios. Es mejor usar generadores que han sido bien analizados a usar los de uno mismo. Aun buenos generadores presentan problemas.
8. Selección de semillas inadecuadas
Los generadores de números aleatorios son procedimientos que dado un numero aleatorio generan otro. El primer numero aleatorio de la secuencia es llamado la semilla y debe ser proporcionada por el analista. Las semillas para diferentes secuencias deben ser cuidadosamente seleccionadas para mantener independencia entre las secuencias. Los analistas usualmente usan una misma secuencia para diferentes procesos o usan la misma semilla para todas las secuencias. Esto introduce correlación entre los procesos y puede llevar a conclusiones erróneas.
II. Otras causas del fracaso de los análisis de simulación
1. Estimación inadecuada del tiempo para desarrollar el proyecto
Es común subestimar el tiempo y el esfuerzo requerido para desarrollar modelos de simulación. Si la simulación es exitosa y produce información útil, sus usuarios quieren incorporar mas funciones, parámetros y detalles. Por el contrario, si no provee de información útil, usualmente se espera que al añadir elementos la puedan hacer útil. En ambos casos el proyecto se extiende mas allá de las proyecciones iniciales. Para proyectos grandes se deben hacer previsiones para incorporara cambios que son inevitables sobre largos periodos de tiempo.
2. Metas inalcanzables
La simulación es un proceso largo y complejo y se debe tener claramente definido un conjunto de metas que sean especificas, minuciosas, medibles, y alcanzables.
Un ejemplo común de una meta inalcanzable es "modelemos X." Es posible modelar muchas características diferentes de X a muchos niveles de detalle.
3. Mezcla incompleta de habilidades
Un proyecto de simulación requiere por lo menos:
a. Liderazgo: Habilidad para motivar, guiar y manejar a los miembros del equipo de simulación.
b. Modelaje y estadísticas: Habilidad para identificar las características claves del sistema y modelarlas al nivel de detalle requerido.
c. Programación: Habilidad para escribir código entendible y verificable que implemente el modelo correctamente.
d. Conocimiento del sistema modelado: Habilidad para entender el sistema, explicarlo al equipo de modelaje, e interpretar los resultados del modelo en términos de su impacto en el diseño del sistema.
4. Nivel inadecuado de participación de los usuarios
Es esencial que el equipo de simulación y los usuarios de la organización estén en constante contacto para intercambiar y discutir ideas. La mayoría de los sistemas evolucionan y cambian con el tiempo y un modelo desarrollado sin la participación de los usuarios raramente resulta exitoso.
5. Documentación inexistente u obsoleta
La mayoría de los modelos de simulación se desarrollan en largos periodos de tiempo y continuamente son modificados a medida que el sistema cambia o es mejor comprendido. Su documentación muchas veces es desatendida y rápidamente se vuelve obsoleta. Es recomendable documentar los programas y usar lenguajes que sean fáciles de leer.
6. Inhabilidad para gerenciar el desarrollo de programas de computación grandes
Hay muchas herramientas de ingeniería de la programación que permiten vigilar los objetivos del diseño, los requerimientos funcionales, las estructuras de datos y los estimados de progreso. También hay un conjunto de principios de diseño, como diseño de arriba abajo y programación estructurada, para desarrollar grandes proyectos en forma ordenada . Sin el uso de estas herramientas y técnicas es imposible desarrollar exitosamente un modelo de simulación grande.
7. Resultados misteriosos
Resultados misteriosos generalmente son debido a errores de programación, supuestos incorrectos en el modelo, o falta de entendimiento del sistema real. Nunca deben ser obviados.
III. Terminología
1. Variables de Estado
El estado del sistema esta caracterizado por el valor que tengan las variables de estado en un instante de tiempo dado. El conjunto de variables de estado debe ser suficiente para el propósito de estudio, y puede diferir en el número y tipo de variables si los objetivos de la simulación cambian. Si la simulación es detenida, puede ser continuada después si y solo si los valores de las variables de estado son conocidos.
2. Evento
Un evento es un suceso, un hecho, una ocurrencia que genera un cambio en el estado del sistema. Una llegada, una salida, etc.
3. Modelos de Tiempo Continuo y de Tiempo Discreto
Modelo de Tiempo Continuo
Cuando el estado del sistema esta definido para cada instante de tiempo.
Modelo de Tiempo Discreto
Cuando el estado del sistema esta definido solo para particulares instantes de tiempo.
4. Modelos de Estado Continuo y de Estado Discreto
El modelo es de estado continuo o discreto dependiendo de si las variables de estado son continuas o discretas.
Modelo de Estado Discreto → Modelo de Eventos Discretos
Modelo de Estado Continuo → Modelo de Eventos Continuos
Continuidad de tiempo no implica continuidad de estado y viceversa.
5. Modelos Determinísticos y Probabilísticos
Si los resultados de un modelo pueden predecirse con certeza, el modelo es determinístico; un simulador de contratos colectivos. Si repeticiones con la misma entrada pueden producir resultados distintos entonces el modelo es probabilístico; un simulador de colas.
6. Modelos Estáticos y Dinámicos
Un modelo en el que el tiempo no es una variable es estático. Si el sistema cambia con el tiempo el modelo es dinámico.
E = m c2 → Modelo Estático (materia en energía) Numero de trabajos en cola en un computador. → Modelo Dinámico
7. Modelos Lineales y No-Lineales
Si la salida es una función lineal de la entrada, el modelo es lineal, de lo contrario es no-lineal.
Ejemplo:
8. Modelos Cerrados y Abiertos
Si la entrada es externa al modelo e independiente de el, el modelo es abierto. Si el modelo es cerrado no hay entrada externa. Puede depender de los objetivos de la simulación, como se enfoque el problema y los supuestos que se hagan. Por ejemplo: podemos simular el trafico en una ciudad como un sistema cerrado si asumimos que el numero de vehículos permanece constante (no hay arribos ni salidas o arribos = salidas), o como un sistema abierto generando arribos y salidas al exterior.
9. Modelo Estables e Inestables
Si el comportamiento del sistema converge a un estado estable (independientemente del tiempo) el modelo es estable. Un modelo cuyo comportamiento cambia constantemente es inestable. Por ejemplo, en un sistema de taquilla simple tenemos:
Intervalo entre llegadas >tiempo de servicio → modelo estable
Intervalo entre llegadas ≤tiempo de servicio → modelo inestable.
Ejemplo
Modelos de sistema de computación generalmente son de tiempo continuo, estado discreto, probabilísticos, dinámicos y no-lineales. Algunos son abiertos y otros cerrados. También pueden ser estables o inestables.
Fuente: Prof. Herbert Hoeger. http://webdelprofesor.ula.ve/ingenieria/hhoeger